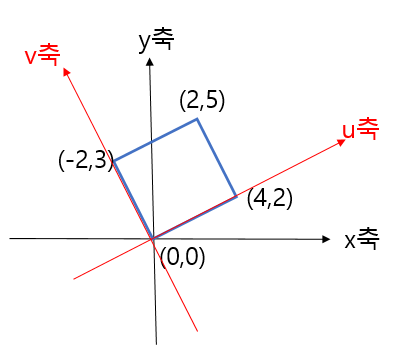
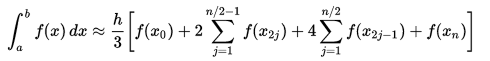이 문제는 경로에 무관한 선적분을 이용하여 풀 것이다.사용할 식은 아래와 같다.F1dx+F2dyF1dx+F2dy 가 완전미분이면 dϕ=F1dx+F2dydϕ=F1dx+F2dy 를 만족하는 함수 ϕϕ 가 존재하므로 ∫CF1dx+F2dy=∫BAdϕ=ϕ(B)−ϕ(A)∫CF1dx+F2dy=∫BAdϕ=ϕ(B)−ϕ(A) - ( 솔직한 공학수학) 이 문제에서 F1=exsiny+x,F2=excosy+tan−1yF1=exsiny+x,F2=excosy+tan−1y 이다.∂F1∂y=excosy=∂F2∂x=excosy∂F1∂y=excosy=∂F2∂x=excosy 이기 때문에 임의의 영역에서 완전미분 가능하다. $..